Calculating square roots is a fundamental math skill, but manually simplifying radicals or finding decimal approximations can be time-consuming. A Square Root Calculator is a handy online tool that provides instant results, whether you need an exact simplified form (like 2√10) or a precise decimal approximation (like 6.32456).

Have you ever wondered about the origin of the square root symbol √? We can assure you that its history is not as simple as you might think. The origin of the root symbol goes back to ancient times, as does the origin of the percent.

The square root symbol was taken from the Arabic letter ج that was placed in its original form of ﺟ in the word جذر — root (the Arabic language is written from right to left).

Roots of cubic polynomial calculator

How Our Square Root Calculator Works

1. Simple Input

Just type any positive number (e.g., 40, 75, 200) into the calculator.

2. Instant Results

Get two forms of the answer:

• Simplified radical (√40 = 2√10)
• Decimal approximation (≈ 6.32456)

3. Detailed Steps

(Example: For √40, it shows: √40 = √(4 × 10) = √4 × √10 = 2√10 ≈ 6.32456)

How is Square Root calculated

Square roots are fundamental in mathematics, but how is a square root calculated exactly? Whether you are using a calculator, computer, or doing it manually, there are several methods to determine square roots. Let’s explore the most common techniques.

1- The Babylonian Method (Heron’s Method)

1. Start with an initial guess (x₀)
2. Improve the guess using:

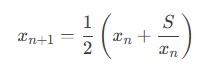
(where S is the number we’re rooting)

3. Repeat until the answer stabilizes

Example for √40:

• Guess x₀ = 6
• x₁ = ½(6 + 40/6) = ½(6 + 6.666…) = 6.3333
• x₂ = ½(6.3333 + 40/6.3333) ≈ 6.3246
• Converges to ≈ 6.324555 (actual √40 ≈ 6.324555320336759)

2- Guess-and-Check (Trial and Error)

1. Make an initial guess (e.g., for √40, guess 6 since 6² = 36)
2. Square the guess (6 × 6 = 36)
3. Compare to the target number (36 < 40 → too low)
4. Adjust the guess upward (try 6.3 → 6.3² = 39.69)
5. Repeat until sufficiently accurate

3- Long Division Method

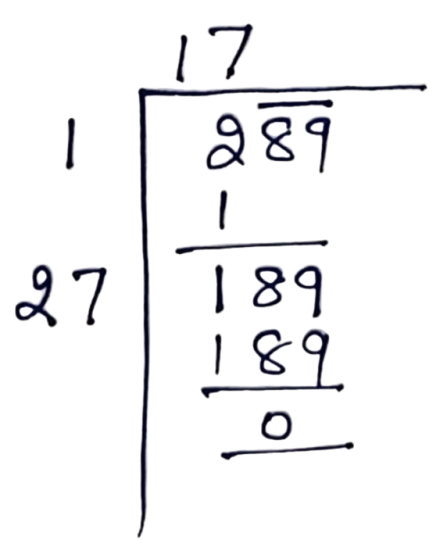
1. Group digits in pairs from the decimal point
2. Find the largest square ≤ first group
3. Subtract and bring down the next pair
4. Double the current result for the new divisor
5. Find next digit where (divisor + digit) × digit ≤ remainder
6. Repeat for the desired precision

4- Logarithmic Method

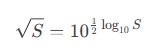
• Convert the square root to an exponent/logarithm problem
• Requires log tables or calculator with log functions

How to find the Square Root

If you facing problems finding out the Square Root, we think that the best answer to the question of how to find the square root is to use the square root calculator. You can use it on your computer and smartphone to quickly estimate the square root of a given number. Unfortunately, there are sometimes situations when you can only depend on yourself. To prepare for this, you should remember several basic perfect square roots:

1. Square root of 1: √1 = 1;
2. Square root of 2: √2 ≈ 1.414214;
3. Square root of 3: √3 ≈ 1.73205;
4. Square root of 4: √4 = 2;
5. Square root of 5: √5 ≈ 2.236068;
6. Square root of 6: √6 ≈ 2.449490;
7. Square root of 7: √7 ≈ 2.645751;
8. Square root of 8: √8 = 2√2 ≈ 2.828427;
9. Square root of 9: √9 = 3;
10. Square root of 10: √10 ≈ 3.162278;
11. Square root of 11: √11 ≈ 3.316625;
12. Square root of 12: √12 = 2√3 ≈ 3.464102;
13. Square root of 13: √13 ≈ 3.605551;
14. Square root of 14: √14 = √14 ≈ 3.741657;
15. Square root of 15: √15 ≈ 3.872983;
16. Square root of 16: √16 = 4;
17. Square root of 17: √17 ≈ 4.123106;
18. Square root of 18: √18 = 3√2 ≈ 4.242641;
19. Square root of 19: √19 ≈ 4.358899;
20. Square root of 20: √20 = 2√5 ≈ 4.472136;
21. Square root of 21: √21 ≈ 4.582576;
22. Square root of 22: √22 ≈ 4.690416;
23. Square root of 23: √23 ≈ 4.795832;
24. Square root of 24: √24 = 2√6 ≈ 4.898979;
25. Square root of 25: √25 = 5;
26. Square root of 26: √26 ≈ 5.099020;
27. Square root of 27: √27 = 3√3 ≈ 5.196152;
28. Square root of 28: √28 = 2√7 ≈ 5.291503;
29. Square root of 29: √29 ≈ 5.385165;
30. Square root of 30: √30 ≈ 5.477226;
31. Square root of 31: √31 ≈ 5.567764;
32. Square root of 32: √32 = 4√2 ≈ 5.656854;
33. Square root of 33: √33 ≈ 5.744563;
34. Square root of 34: √34 ≈ 5.830952;
35. Square root of 35: √35 ≈ 5.916080;
36. Square root of 36: √36 = 6;
37. Square root of 37: √37 ≈ 6.082763;
38. Square root of 38: √38 ≈ 6.164414;
39. Square root of 39: √39 ≈ 6.244998;
40. Square root of 40: √40 = 2√10 ≈ 6.324555;
41. Square root of 41: √41 ≈ 6.403124;
42. Square root of 42: √42 ≈ 6.480741;
43. Square root of 43: √43 ≈ 6.557439;
44. Square root of 44: √44 = 2√11 ≈ 6.633250;
45. Square root of 45: √45 = 3√5 ≈ 6.708204;
46. Square root of 46: √46 ≈ 6.782330;
47. Square root of 47: √47 ≈ 6.855655;
48. Square root of 48: √48 = 4√3 ≈ 6.928203;
49. Square root of 49: √49 = 7;
50. Square root of 50: √50 = 5√2 ≈ 7.071068;
51. Square root of 64: √64 = 8;
52. Square root of 81: √81 = 9;
53. Square root of 100: √100 = 10;
54. Square root of 121: √121 = 11;
55. Square root of 144: √144 = 12;

Frequently Asked Questions (FAQ)

Ques-1.- Is the square root of 2 a rational number?

No, the square root of 2 is not rational. This is because when 2 is written as a fraction, ²/₁, it can never have only even exponents, and therefore a rational number cannot have been squared to create it.

Ques-2. Is square roots rational ?

Some square roots are rational, whereas others are not. You can determine if a square root is rational by finding out if the number you are square rooting can be expressed in terms of only even exponents (e.g., 4 = 2² / 1²). If it can, its root is rational.

Ques-3. Is 144 a perfect square?

Yes, the number 144 is a perfect square. It can be written as an integer with itself (12×12=144), which is a perfect square’s property. Perfect squares are numbers that have an integer value as a square root, and in this case, the square root of 144 is 12, which is an integer.